Attention Mechanism in Transformers

This overview delves into the transformative role of attention mechanisms in the architecture of advanced language models, specifically the transformer model. Beginning with a discussion on word embeddings and the basic self-attention mechanism, the text explores how attention is harnessed to extract long-range relationships within word sequences. From the fundamental principles of dot product attention and scaled dot product attention to the multi-head attention, this deep dive reveals how attention enables natural language understanding.

Introduction

Today’s advanced language models are based on transformer architecture . The transformer architecture, which is otherwise no different from MLP (multilayer perceptron), relies on the attention mechanism. Attention provides the network with the ability to extract long-range relationships within given word sequences which is crucial in natural language understanding. Prior to the main discussion, I will briefly explain word embeddings. To keep things simple, I will introduce “the basic self-attention” which I call it in that way as it is the simplest form of self-attention. Then, I will elaborate on scaled dot product attention and multi-head attention.

Attention is a general term and can be in different forms, e.g. additive attention . Throughout this text, attention refers to the “dot product attention”. It should be also noted that self-attention is a form of attention focusing on the relationships “within” the sequence.

Word embedding

Word embedding is a representation of words (or tokens) as vectors in high-dimensional space. This representation can be learned from a large corpus for example using word2vec methods so that resulting embedding vectors encode semantic relationships within the corpus. Specifically, embedding vectors of two semantically related words are expected to be similar in terms of direction assuming that all embedding vectors are of unit length. Figure 1 illustrates word vectors in three-dimensional space. Such learned representation of words can also reflect indirect relationships. For example, the vector differences (woman-man) and (queen-king) are expected to be similar which are shown in red in Figure 1.

Figure 1. Illustration of word vectors in three-dimensional embedding space.

Basic self-attention

I use the basic self-attention term to refer to the simplest form of self-attention. Equation \eqref{eq:basic-sa} is the mathematical expression of basic self-attention where \(x\) represents a sequence of words as illustrated in Figure 2, \(d_s\) is the sequence length which is the number of words (or tokens) in the input sequence, and \(d_m\) is the dimensionality of the word embedding.

\begin{equation} \label{eq:basic-sa} A=\operatorname{softmax}\left(x x^{\top}\right) x \text { where } x \in \mathbb{R}^{d_s \times d_m} \end{equation}

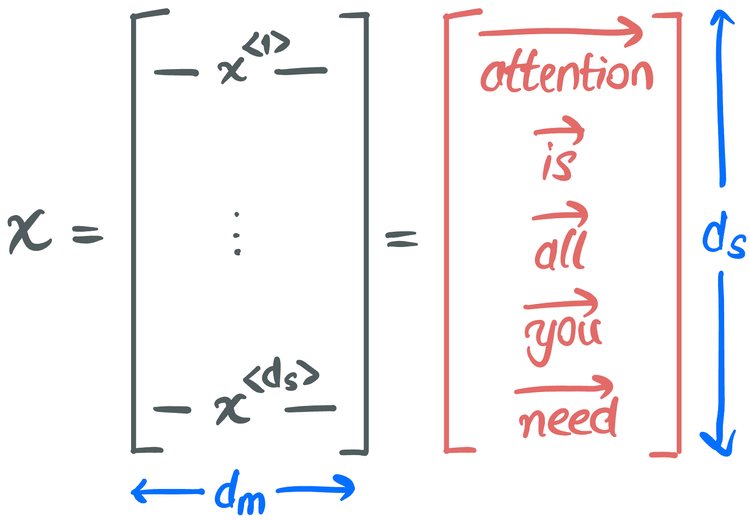
Figure 2. An example input sequence to transformers. For simplicity, the example sequence is at the word level, not the token level.

The expression \(softmax(xx^\top)x\) can be understood in three steps:

\(xx^\top\): similarity scores between each word.
\(softmax(xx^\top)\): convert similarity scores into weights. At this step, similarity scores are converted into values between 0 and 1.
\(softmax(xx^\top)x\): weighted sum of features from input itself (self-attention).

Let’s explore each step in detail. Equation \eqref{eq:similarities} shows the matrix multiplication to compute similarity scores between words. \(x^i x^{j \top}\) gives the similarity score between the \(i\)th and \(j\)th words in the sequence. Thus, for dₛ words, there are \(d_s \times d_s\) scores. Note that \(xx^\top\) is a symmetric matrix.

\begin{equation} \label{eq:similarities} x x^{\top} = \begin{bmatrix} x^{\langle 1 \rangle}
\vdots
x^{\langle d_s \rangle} \end{bmatrix} \begin{bmatrix} x^{\langle 1 \rangle^{\top}} & \cdots & x^{\langle 1 \rangle^{\top}}
\vdots & \ddots & \vdots
x^{\langle d_s \rangle^{\top}} & \cdots & x^{\langle d_s \rangle^{\top}} \end{bmatrix} = \begin{bmatrix} x^{\langle 1 \rangle} \cdot x^{\langle 1 \rangle^{\top}} & \cdots & x^{\langle 1 \rangle} \cdot x^{\langle d_s \rangle^{\top}}
\vdots & \ddots & \vdots
x^{\langle d_s \rangle} \cdot x^{\langle 1 \rangle^{\top}} & \cdots & x^{\langle d_s \rangle} \cdot x^{\langle d_s \rangle^{\top}} \end{bmatrix} \text{ where } x x^{\top} \in \mathbb{R}^{d_s \times d_s} \end{equation}

The cosine similarity given in Equation \eqref{eq:cos-sim} equals the dot product for vectors of unit length. Therefore, \(x^i x^{j \top}\) is essentially the cosine similarity between two word vectors.

\begin{equation} \label{eq:cos-sim} \cos (\theta)=\frac{\mathbf{A} \cdot \mathbf{B}}{|\mathbf{A}||\mathbf{B}|} \end{equation}

Cosine similarity is a measure of how similar two vectors are. When two vectors are similar, the angle (θ) between them is small meaning that cos(θ) is large which is bounded by 1. Therefore, dot product is proportional to vector similarity as given in Equation \eqref{eq:similarities}.

In the second step, we apply softmax to similarity scores as given in Equation \eqref{eq:softmax} where \(P\) is a \(d_s \times d_s\) matrix. \(P^i\) is the similarity of the \(i\)th word to each word in the sequence such that the sum of all elements of \(P^i\) makes up 1. In that sense, similarity scores are converted into weights using softmax.

\begin{equation} \label{eq:softmax} P = \text{softmax}\left(x x^{\top}\right) = \begin{bmatrix} P^{\langle 1 \rangle}
\vdots
P^{\langle d_s \rangle} \end{bmatrix} \end{equation}

The last step is basically a weighted sum. Using similarity scores, each word is reconstructed considering its relationship with all words in the sequence. Specifically, the \(k\)th feature (or element) of the \(i\)th word in the sequence is determined by the dot product between \(P^i\) and \(x_k\) where \(x_k\) is the \(k\)th column of input \(x\). This dot product is basically the expectation over feature dimensions using similarity scores as weights. In this way, the new representation of the \(i\)th word encodes its similarity to each word in the sequence. Figure 3 summarizes the weighted sum step.

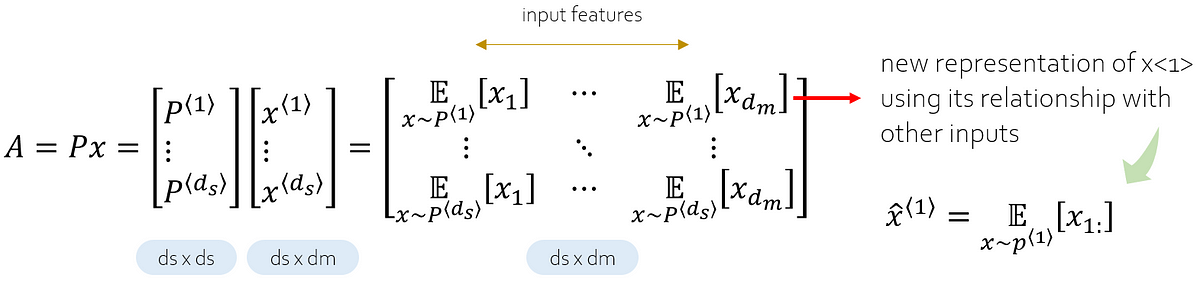
Figure 3. Weighted sum step in basic self-attention.

For example, considering the input sequence given in Figure 2, the first feature of the resulting representation of the word attention is determined by the weighted sum of the first features of all words in the sequence using similarity scores.

Figure 4 demonstrates a numerical example of the three steps of basic self-attention which summarizes the concept. The embedding space is assumed to be three-dimensional. In the example, the word vectors do not represent learned embeddings, they are instead random.

Figure 4. A numerical example of the three steps of basic self-attention.

Dot Product Attention

The mathematical expression of dot product attention is given in Equation (5) where \(Q\), \(K\), and \(V\) are called query, key, and value, respectively, inspired by databases.

\begin{equation} \label{eq:A} A=\operatorname{softmax}\left(Q K^{\top}\right) V \end{equation}

This is the generalized form of self-attention as when \(Q = K = V\), then the operation becomes self-attention and focuses on the relationships within the sequence. However, in the generalized form, attention can be performed on two different sequences. For example, assume that \(Q\) is from sequence 1, and \(K\) and \(V\) are from sequence 2. This implies that sequence 2 is going to be reconstructed using its relationships with sequence 1 which is what happens in the encoder-decoder attention layers of the transformer.

Scaled dot product attention

Scaled dot product attention given in Equation (6) is a slightly modified version of dot product attention such that similarity scores (\(QK^\top\)) are scaled by \(\sqrt{d_k}\). The reason is that assuming that \(Q\) and \(K\) are of shape \(d_s \times d_k\) and they are independent random variables with mean 0 and variance 1, their dot product has mean 0 and variance \(d_k\). Note that \(d_s\) is the sequence length and \(d_k\) is the feature dimensionality. With this modification, changes in \(d_k\) do not create a problem.

\begin{equation} \label{eq:attention} \operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) V \end{equation}

Multi-head attention

Multi-head attention is an extended form of scaled dot product attention with learnable parameters in a multi-headed manner. Figure 5 shows attention with prior linear transformations. \(W_i^Q\), \(W_i^K\), and \(W_i^V\) are learnable parameters and are realized as linear layers.

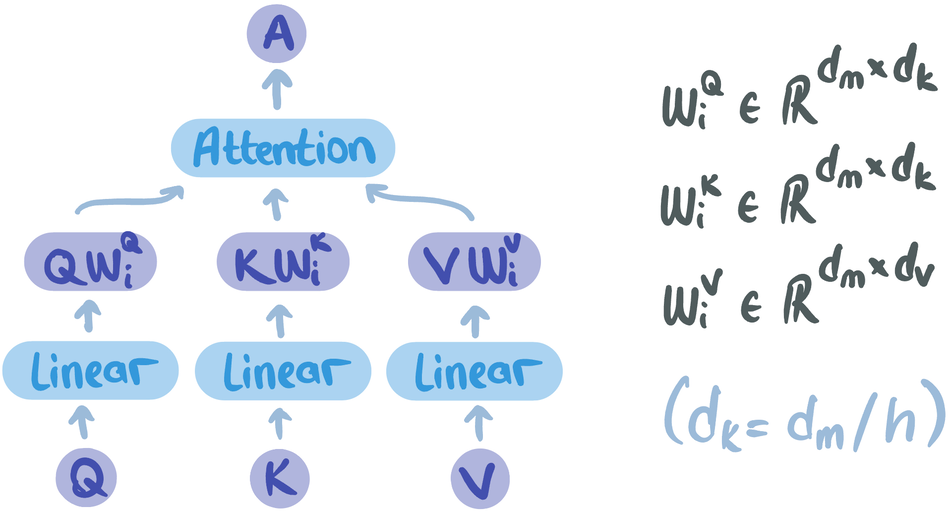
Figure 5. Attention with prior linear transformations.

Intuitively, the resulting matrices after linear transformations are more useful (or richer) representations of input sequences such that the similarity scores and weighted sum step can be improved via learning. Figure 6 illustrates the overall multi-head attention. The input sequences, \(Q\), \(K\), and \(V\), are of shape \(d_s \times d_m\). After linear transformations, the resulting matrices have \(d_k\) dimension in feature space (generally \(d_v = d_k\)). After performing attention over transformed matrices, the resulting matrix is of shape \(d_s \times d_k\) and there are h of them such that \(i = \{1,…,h\}\). They are concatenated such that \(d_s \times (d_k \times h)\) becomes \(d_s \times d_m\). Finally, another linear transformation is performed on the resulting matrix.

Figure 6. Multi-head attention.

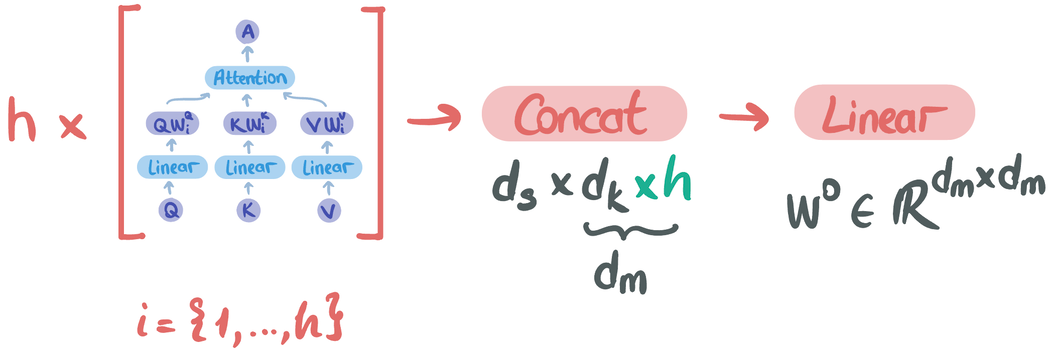
It should be noted that multi-head attention is implemented in the form of self-attention in the encoder and decoder parts of the transformer architecture as queries (Q), keys (K), and values (V) are the same. In the encoder-decoder attention layers, keys and values come from the encoder part, and queries come from the decoder part as explained in the dot product attention part by an example.

The multi-head form of attention provides the transformer with the ability to focus on associations within sequences (or between sequences) considering different aspects, i.e. semantic and syntactic.

Conclusion

In this text, the attention mechanism, i.e. multi-head attention, of the transformer architecture was elucidated. The method relies on the cosine similarity between word vectors. Multi-head attention can extract long-range relationships within or between sequences. Not only in texts but also in images , attention can be used.